联系我们
- 上海耐创测试技术有限公司
- 联系人:陈工
- 电话:021-39197548
- 邮箱:zhujing@forcechina.com
- 地址:上海市嘉定区马陆镇宝安公路2999弄东方慧谷50号2层

基于矩阵补偿方法的串扰修正
文章出处:NaiChuang人气:发表时间:2021-06-18 14:28:21
基于矩阵补偿方法的串扰修正
美国SDI公司 David Schrand
力/力矩传感器设计用于【沿着定义的轴向,通常标记为X,Y和Z】测量力和力矩。这些力/力矩传感器由1~6个通道;6通道的力/力矩传感器包含三个通道的力Fx,Fy,Fz和三个通道的力矩Mx,My,Mz;
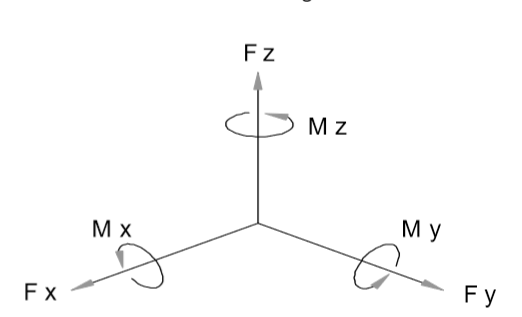
理想状态是,一个测量轴上的负载将不会在其它任何测量通道上产生输出。
现实是,没有任何多轴向传感器可以做到这种互不干扰;
对于大多数的多通道传感器而言,这种不需要的输出,我们称之为串扰,一般在1%~5%之间;虽然1%~5%的串扰听起来不多,但是对于有六个通道的力/力矩传感器而言,每一个通道都会有来自其它五个通道的串扰,这种串扰叠加在一起就可能造成5%~25%的串扰输出;
基本上,有两种办法来减少由多通道之间的串扰带来的测量误差:
第一种方法是在传感器后端加补偿电路和对传感器机械结构进行改良,以求达到减小【非测量轴的外来负载引起的通道输出】;这种方法虽然有效,但是如果要补偿两个通道以上的外部负载,这种方法是耗时且不切实际的;
第二种是通过数学方法,对各个轴向的负载输出进行解析校准来得出正确的通道输出值,这种方法对于任何数量的外部载荷都是有效的,并且可以通过应用“交叉耦合系数”或逆矩阵方法来表征为数学串扰补偿。
我们将要讲的就是矩阵系数方法。
当负载施加到力传感器时,与该负载对应的测量通道将响应输出。然而,如前所述,与施加的负载轴向不一致的其他测量通道也将对该负载做出响应。这是坏消息,好消息是,对于任何给定的负载或负载组合,该响应是可重复的。这意味着通过在校准过程中仔细地应用这些无关的负载,并记录每个通道输出响应到这些负载,可以创建传感器的输出轮廓。
从这里,可以创建一系列联立方程来描述力传感器的串扰性能。通过使用来自传感器的所有通道的任何一组同时数据来求解该系列方程,可以确定产生该唯一数据集的真实负载条件。该方法的缺点在于,需要加载标定传感器的所有轴向。这通常不是问题,因为在大多数情况下,我们可以在加载的同时用数据采集设备监测每一个通道的输出。
OFx = K1 ·Fx
同时,其他五个通道的输出将被记录为串扰输出。现在传感器的传递功能开始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
通过这一组方程,可以通过将传感器输出除以施加的负载来确定每个轴的传递函数(K1,K7等)。
将使用相同的过程来校准传感器的剩余五个轴,提供剩余的传递函数。 使用叠加理论,可以组合产生完全描述传感器对所有施加载荷的输出的输出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
这些方程式描述了传感器在施加的载荷方面的输出。 然而,在应用中,负载是未知数,输出是已知的测量量。 利用这六个方程及其六个未知数(载荷Fx-z和Mx-z),可以解决未知载荷;
【逆矩阵方法】
可以通过使用所谓的逆矩阵法来解决上述的一系列方程式。反矩阵理论,我们可以参考线性代数中的逆矩阵求法来取得【K·K-1=E】。实质上,这是一种“反转”方程式的技术,使得不再像上述那样将输出作为负载的函数,所以负载现在是输出的功能。
用于纠正或补偿由于串扰错误导致的传感器输出的逆矩阵涉及到收集传感器上的校准数据对外部负载的响应,并使用它构建可用于找到传感器真实负载条件的矩阵。已经经过彻底校准的多轴传感器将已经具有提供校准数据的这种串扰矩阵。有关创建此矩阵涉及的步骤的更多信息,请参见附录B“查找逆矩阵”。
这可能看起来很混乱,但是处理一个非常复杂的问题是一个非常简单的方法。例如,我们有一个“不太完美”的传感器。然而,我们确实提供了传感器提供的串扰矩阵,如下所示。
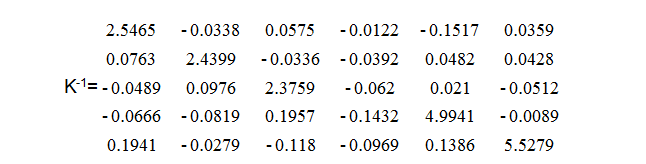
X = K-1·O
使用该逆矩阵,可以计算产生来自传感器的任何一组同时数据的负载。 我们从逆矩阵K-1和方程式开始:
X = K-1·O
或者展开写:
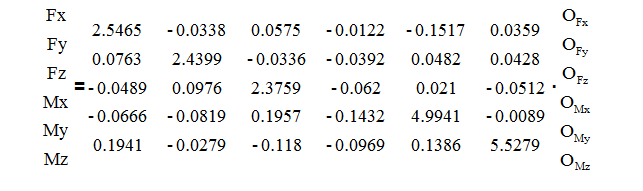
OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的时间,我们从传感器获取以上数据
要找到必须存在的Fx负载来创建这六个输出,我们将逆矩阵的第一行的元素乘以所记录的各个输出,并将它们相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
类似的,可以通过对逆矩阵的剩余五行执行相同的操作来计算剩余的五个负载,这样就能得出一个完整传感器的加载概况;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
在实际使用中,这些计算可以通过数据采集或控制系统实时设置,也可以通过使用电子表格程序在测试完成后对数据进行后处理来完成。 这种技术通常会将串扰减少到传感器满量程的0.5%。
美国SDI公司 David Schrand
力/力矩传感器设计用于【沿着定义的轴向,通常标记为X,Y和Z】测量力和力矩。这些力/力矩传感器由1~6个通道;6通道的力/力矩传感器包含三个通道的力Fx,Fy,Fz和三个通道的力矩Mx,My,Mz;

理想状态是,一个测量轴上的负载将不会在其它任何测量通道上产生输出。
现实是,没有任何多轴向传感器可以做到这种互不干扰;
对于大多数的多通道传感器而言,这种不需要的输出,我们称之为串扰,一般在1%~5%之间;虽然1%~5%的串扰听起来不多,但是对于有六个通道的力/力矩传感器而言,每一个通道都会有来自其它五个通道的串扰,这种串扰叠加在一起就可能造成5%~25%的串扰输出;
基本上,有两种办法来减少由多通道之间的串扰带来的测量误差:
第一种方法是在传感器后端加补偿电路和对传感器机械结构进行改良,以求达到减小【非测量轴的外来负载引起的通道输出】;这种方法虽然有效,但是如果要补偿两个通道以上的外部负载,这种方法是耗时且不切实际的;
第二种是通过数学方法,对各个轴向的负载输出进行解析校准来得出正确的通道输出值,这种方法对于任何数量的外部载荷都是有效的,并且可以通过应用“交叉耦合系数”或逆矩阵方法来表征为数学串扰补偿。
我们将要讲的就是矩阵系数方法。
当负载施加到力传感器时,与该负载对应的测量通道将响应输出。然而,如前所述,与施加的负载轴向不一致的其他测量通道也将对该负载做出响应。这是坏消息,好消息是,对于任何给定的负载或负载组合,该响应是可重复的。这意味着通过在校准过程中仔细地应用这些无关的负载,并记录每个通道输出响应到这些负载,可以创建传感器的输出轮廓。
从这里,可以创建一系列联立方程来描述力传感器的串扰性能。通过使用来自传感器的所有通道的任何一组同时数据来求解该系列方程,可以确定产生该唯一数据集的真实负载条件。该方法的缺点在于,需要加载标定传感器的所有轴向。这通常不是问题,因为在大多数情况下,我们可以在加载的同时用数据采集设备监测每一个通道的输出。
OFx = K1 ·Fx
同时,其他五个通道的输出将被记录为串扰输出。现在传感器的传递功能开始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
通过这一组方程,可以通过将传感器输出除以施加的负载来确定每个轴的传递函数(K1,K7等)。
将使用相同的过程来校准传感器的剩余五个轴,提供剩余的传递函数。 使用叠加理论,可以组合产生完全描述传感器对所有施加载荷的输出的输出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
这些方程式描述了传感器在施加的载荷方面的输出。 然而,在应用中,负载是未知数,输出是已知的测量量。 利用这六个方程及其六个未知数(载荷Fx-z和Mx-z),可以解决未知载荷;
【逆矩阵方法】
可以通过使用所谓的逆矩阵法来解决上述的一系列方程式。反矩阵理论,我们可以参考线性代数中的逆矩阵求法来取得【K·K-1=E】。实质上,这是一种“反转”方程式的技术,使得不再像上述那样将输出作为负载的函数,所以负载现在是输出的功能。
用于纠正或补偿由于串扰错误导致的传感器输出的逆矩阵涉及到收集传感器上的校准数据对外部负载的响应,并使用它构建可用于找到传感器真实负载条件的矩阵。已经经过彻底校准的多轴传感器将已经具有提供校准数据的这种串扰矩阵。有关创建此矩阵涉及的步骤的更多信息,请参见附录B“查找逆矩阵”。
这可能看起来很混乱,但是处理一个非常复杂的问题是一个非常简单的方法。例如,我们有一个“不太完美”的传感器。然而,我们确实提供了传感器提供的串扰矩阵,如下所示。

X = K-1·O
使用该逆矩阵,可以计算产生来自传感器的任何一组同时数据的负载。 我们从逆矩阵K-1和方程式开始:
X = K-1·O
或者展开写:

OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的时间,我们从传感器获取以上数据
要找到必须存在的Fx负载来创建这六个输出,我们将逆矩阵的第一行的元素乘以所记录的各个输出,并将它们相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
类似的,可以通过对逆矩阵的剩余五行执行相同的操作来计算剩余的五个负载,这样就能得出一个完整传感器的加载概况;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
在实际使用中,这些计算可以通过数据采集或控制系统实时设置,也可以通过使用电子表格程序在测试完成后对数据进行后处理来完成。 这种技术通常会将串扰减少到传感器满量程的0.5%。













 沪公网安备 31011402003414号
沪公网安备 31011402003414号