联系我们
- 上海耐创测试技术有限公司
- 联系人:陈工
- 电话:021-39197548
- 邮箱:zhujing@forcechina.com
- 地址:上海市嘉定区马陆镇宝安公路2999弄东方慧谷50号2层

基于矩阵补偿方法的串扰修正
文章出处:未知人气:发表时间:2017-07-26 13:30:18
CROSS-TALK COMPENSATION USING MATRIX METHODS
基于矩阵补偿方法的串扰修正
David Schrand, SDI Inc.
美国SDI公司 David Schrand
力/力矩传感器设计用于【沿着定义的轴向,通常标记为X,Y和Z】测量力和力矩。这些力/力矩传感器由1~6个通道;6通道的力/力矩传感器包含三个通道的力Fx,Fy,Fz和三个通道的力矩Mx,My,Mz;
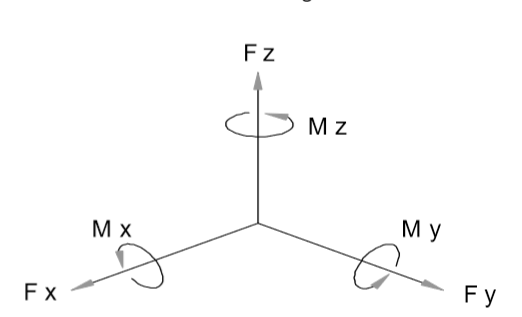
理想状态是,一个测量轴上的负载将不会在其它任何测量通道上产生输出。
现实是,没有任何多轴向传感器可以做到这种互不干扰;
对于大多数的多通道传感器而言,这种不需要的输出,我们称之为串扰,一般在1%~5%之间;虽然1%~5%的串扰听起来不多,但是对于有六个通道的力/力矩传感器而言,每一个通道都会有来自其它五个通道的串扰,这种串扰叠加在一起就可能造成5%~25%的串扰输出;
There are basically two methods used to reduce this potential source of measurement error. With the first method, the load-cell is ‘tuned’, either mechanically or electrically to reduce the channels output due to off-axis or extraneous loads. While effective, this method is time consuming and is not practical if more than two extraneous loads need to be compensated for. The other method of cross-talk compensation involves mathematically manipulating the load-cells output data to correct the cross-talk outputs. It is effective for any number of extraneous loads, and can be characterized as mathematical cross-talk compensation by the application of “cross coupling coefficients”, or the inverse matrix method. This is the method that will be discussed here.
基本上,有两种办法来减少由多通道之间的串扰带来的测量误差:
第一种方法是在传感器后端加补偿电路和对传感器机械结构进行改良,以求达到减小【非测量轴的外来负载引起的通道输出】;这种方法虽然有效,但是如果要补偿两个通道以上的外部负载,这种方法是耗时且不切实际的;
第二种是通过数学方法,对各个轴向的负载输出进行解析校准来得出正确的通道输出值,这种方法对于任何数量的外部载荷都是有效的,并且可以通过应用“交叉耦合系数”或逆矩阵方法来表征为数学串扰补偿。
我们将要讲的就是矩阵系数方法。
When a load is applied to a force sensor, the measurement channel that lines up with that load will respond. However, as described earlier, other measurement channels that are not in line with that applied load will also respond to that load. That’s the bad news. The good news is that that response is repeatable for any given load or combination of loads. This means that by carefully applying these extraneous loads during the calibration process, and recording each channels output response to those loads, an output profile of the sensor can be created. From here, a series of simultaneous equations can be created to describe the cross talk performance of the force sensor. By solving this series of equations using any set of simultaneous data from all the channels of the sensor, the true loading condition that produced that unique set of data can be determined. The drawback to this method is that a sensor channel is required for each extraneous load that is present during loading. This usually isn’t a problem, since in most instances, a measurement channel is present to monitor all the significant loads present in the application
当负载施加到力传感器时,与该负载对应的测量通道将响应输出。然而,如前所述,与施加的负载轴向不一致的其他测量通道也将对该负载做出响应。这是坏消息,好消息是,对于任何给定的负载或负载组合,该响应是可重复的。这意味着通过在校准过程中仔细地应用这些无关的负载,并记录每个通道输出响应到这些负载,可以创建传感器的输出轮廓。
从这里,可以创建一系列联立方程来描述力传感器的串扰性能。通过使用来自传感器的所有通道的任何一组同时数据来求解该系列方程,可以确定产生该唯一数据集的真实负载条件。该方法的缺点在于,需要加载标定传感器的所有轴向。这通常不是问题,因为在大多数情况下,我们可以在加载的同时用数据采集设备监测每一个通道的输出。
OFx = K1 ·Fx
At the same time, the output from the other five channels will be recorded as cross talk outputs. Now the transfer functions for the sensor begin to take shape.
同时,其他五个通道的输出将被记录为串扰输出。现在传感器的传递功能开始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
From this set of equations, the transfer functions (K1, K7, etc), can be determined for each axis by dividing the sensors output by the applied load.
通过这一组方程,可以通过将传感器输出除以施加的负载来确定每个轴的传递函数(K1,K7等)。
This same procedure will be used to calibrate the remaining five axes of the sensor, providing the remaining transfer functions. Using the theory of superposition, they can be combined to yield the output equations that fully describe the output of the sensor to all the applied loads
将使用相同的过程来校准传感器的剩余五个轴,提供剩余的传递函数。 使用叠加理论,可以组合产生完全描述传感器对所有施加载荷的输出的输出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
These equations describe the output of the sensor in terms of the applied loads. However, in application, the loads are the unknowns, and the outputs are the known measured quantities. With these six equations and their six unknowns (the loads Fx-z and Mx-z), it will be possible to solve for the unknown loads.
这些方程式描述了传感器在施加的载荷方面的输出。 然而,在应用中,负载是未知数,输出是已知的测量量。 利用这六个方程及其六个未知数(载荷Fx-z和Mx-z),可以解决未知载荷;
【逆矩阵方法】
The series of equations described above can be solved by using what is called the inverse matrix method. A brief overview of the theory behind this technique is given in Appendix A, ‘Inverse Matrix Theory’. In essence, it is a technique that ‘inverts’ the equations so that instead of having the output as a function of the loads as described above, the loads are now functions of the outputs.
Finding the inverse matrix used to correct or compensate a sensors output due to cross talk errors, involves gathering calibration data on the sensors response to extraneous loads, and using it to construct a matrix that can be used to find the sensors true loading condition. A multi-axis sensor that has undergone a thorough calibration, will already have such a cross talk matrix supplied with the calibration data. More information on the steps involved in creating this matrix is presented in Appendix B, ‘Finding the Inverse Matrix’.
This may all seem confusing, but it is a very simple way to handle a very complex problem. For example, we have a sensor that is ‘less than perfect’. We do however have the cross talk matrix that was supplied with the sensor, as listed below.
可以通过使用所谓的逆矩阵法来解决上述的一系列方程式。反矩阵理论,我们可以参考线性代数中的逆矩阵求法来取得【K·K-1=E】。实质上,这是一种“反转”方程式的技术,使得不再像上述那样将输出作为负载的函数,所以负载现在是输出的功能。
用于纠正或补偿由于串扰错误导致的传感器输出的逆矩阵涉及到收集传感器上的校准数据对外部负载的响应,并使用它构建可用于找到传感器真实负载条件的矩阵。已经经过彻底校准的多轴传感器将已经具有提供校准数据的这种串扰矩阵。有关创建此矩阵涉及的步骤的更多信息,请参见附录B“查找逆矩阵”。
这可能看起来很混乱,但是处理一个非常复杂的问题是一个非常简单的方法。例如,我们有一个“不太完美”的传感器。然而,我们确实提供了传感器提供的串扰矩阵,如下所示。
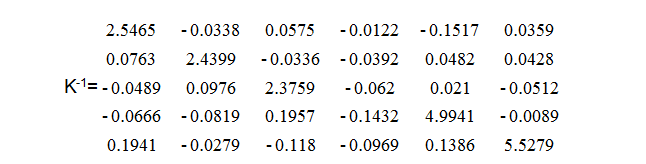
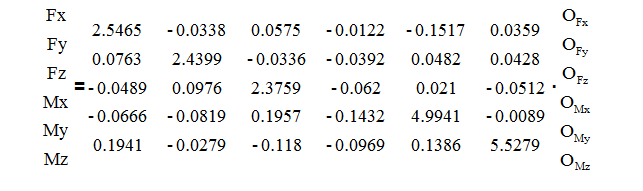
With this inverse matrix the loads that produced any set of simultaneous data from the sensor can be calculated. We start with the inverse matrix, K-1, and the equation:
X = K-1·O
使用该逆矩阵,可以计算产生来自传感器的任何一组同时数据的负载。 我们从逆矩阵K-1和方程式开始:
X = K-1·O
Or, in long hand:
或者展开写:
At a particular point in time, we obtain the following readings from our sensor:
OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的时间,我们从传感器获取以上数据
To find the Fx load that must have been present to create those six outputs, we multiply the elements of the first row of the inverse matrix by the individual outputs that were recorded, and sum them:
要找到必须存在的Fx负载来创建这六个输出,我们将逆矩阵的第一行的元素乘以所记录的各个输出,并将它们相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
Similarly, the remaining five loads can be calculated by carrying out the same operations on the remaining five rows of the inverse matrix. Doing so yields the following loading conditions:
类似的,可以通过对逆矩阵的剩余五行执行相同的操作来计算剩余的五个负载,这样就能得出一个完整传感器的加载概况;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
In actual use, these calculations can be set up to be done in real time by the data acquisition or control system, or can be done by post processing the data after the test is complete by using a spread sheet program. This technique will typically reduce the cross talk to less that 0.5% of the full scale capacities of the sensor.
在实际使用中,这些计算可以通过数据采集或控制系统实时设置,也可以通过使用电子表格程序在测试完成后对数据进行后处理来完成。 这种技术通常会将串扰减少到传感器满量程的0.5%。
知识点回顾:K·K-1=E
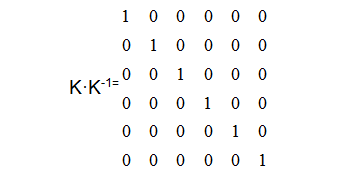
以上就是六维力传感器矩阵系数标定的过程,仅供参考,如有错误请指正!













 沪公网安备 31011402003414号
沪公网安备 31011402003414号